- Unit 3 Basic Differentiationap Calculus 2nd Edition
- Unit 3 Basic Differentiationap Calculus Calculator
7.2 Average and Instantaneous Rates of Change 1 August 30, 2016 Calculus Unit #1: Basic Differentiation 7.2 Average and Instantaneous Rates of Change. 01 - Basic Derivatives in Calculus, Part 1 - Learn what a Derivative is and how to Solve Them. 01 - Basic Derivatives in Calculus, Part 1 - Learn what a Derivative is and how to Solve Them. Door Math and Science 4 jaar geleden 34 minuten 38.745 weergaven This is just a few minutes of a complete course. Unit 1: Function & Trig Review. Unit 2: Limits & Continuity. Unit 3: Differentiation. Unit 3 - Basic Derivative Rules Notes.pdf (125k) Unknown user. AP Calculus AB – Worksheet 20 Limit Definition of the Derivative and the Tangent Line Problem Find the derivative of the function using the limit process. Remember: The derivative is a new function so it requires new notation; Example: ' or or ' dy f x y dx 1 gx 5 2 3 2 3 h s s 3 f x x2 1.
Enter an expression and the variable to differentiate with respect to. Then click the Differentiate button.
Finding the derivative of
involves computing the following limit:
To put it mildly, this calculation would be unpleasant. We would like to find ways to compute derivatives without explicitly using the definition of the derivative as the limit of a difference quotient. A useful preliminary result is the following:
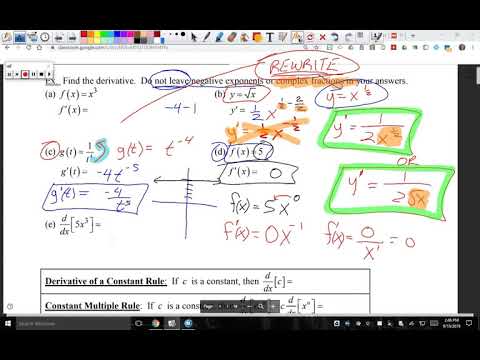
Derivative of a Constant
lf c is any real number and if f(x) = c for all x, then f ' (x) = 0 for all x . That is, the derivative of a constant function is the zero function.
It is easy to see this geometrically. Referring to Figure 1, we see that the graph of the constant function f(x) = c is a horizontal line. Since a horizontal line has slope 0, and the line is its own tangent, it follows that the slope of the tangent line is zero everywhere.
We next give a rule for differentiating f(x) = xn where n is any real number.Some of the following results have already been verified in the previous section, and the
others can be verified by using the definition of the derivative.
This pattern suggests the following general formula for powers of n where n is a positive integer.
Power Rule
In fact, the power rule is valid for any real number n and thus can be used to differentiate a variety of non-polynomial functions. The following example illustrates some applications of the power rule.
Example 1
Differentiate each of the following functions:
Unit 3 Basic Differentiationap Calculus 2nd Edition
(a) Since f(x) = 5, f is a constant function; hence f '(x) = 0.
(b) With n = 15 in the power rule, f '(x) = 15x14
(c) Note that f(x) = x1/2 . Hence, with n = 1/2 in the power rule,
(d) Since f(x) = x-1, it follows from the power rule that f '(x) = -x-2 = -1/x2
The rule for differentiating constant functions and the power rule are explicit differentiation rules. The following rules tell us how to find derivatives of combinations of functions in terms of the derivatives of their constituent parts. In each case, we assume that f '(x) and g'(x) exist and A and B are constants.
The four rules listed above, together with the rule on differentiating constant functions and the power rule, provide us with techniques for differentiating any function that is expressible as a power or root of a quotient of polynomial functions. The next series of examples illustrates this. The linearity rule and the product rule will be justified at the end of the section; a proof of the extended power rule appears in the section on the chain rule.
Example 2 Let
Find f '(x).
Solution Using the linearity rule, we see that
Example 3 Let
Again using linearity,
f'(x) = a(x3)' + b(x2)' + c(x)' + (d)' = 3ax^2 + 2bx + c
Example 3 can be generalized as follows:
A polynomial of degree n has a derivative everywhere, and the derivative is a polynomial of degree (n - 1).
Example 4 Let
Find f '(x).
First we use the product rule, since f(x) is given as the product of x2 and x2 -x + 1:
Some differentiation rules are a snap to remember and use. These include the constant rule, power rule, constant multiple rule, sum rule, and difference rule.
The constant rule: This is simple. f (x) = 5 is a horizontal line with a slope of zero, and thus its derivative is also zero.
The power rule:
To repeat, bring the power in front, then reduce the power by 1. That’s all there is to it.
The power rule works for any power: a positive, a negative, or a fraction.
Make sure you remember how to do the last function. It’s the simplest function, yet the easiest problem to miss. By the way, do you see how finding this last derivative follows the power rule? (Hint: x to the zero power equals one).
You can differentiate radical functions by rewriting them as power functions and then using the power rule.
Unit 3 Basic Differentiationap Calculus Calculator
The constant multiple rule: What if the function you’re differentiating begins with a coefficient? Makes no difference. A coefficient has no effect on the process of differentiation. You just ignore it and differentiate according to the appropriate rule. The coefficient stays where it is until the final step when you simplify your answer by multiplying by the coefficient.
Don’t forget that ð (~3.14) and e (~2.72) are numbers, not variables, so they behave like ordinary numbers. Constants in problems, like c and k,also behave like ordinary numbers. So, for example,
The sum rule: When you want the derivative of a sum of terms, take the derivative of each term separately.
The difference rule: If you have a difference (that’s subtraction) instead of a sum, it makes no difference. You still differentiate each term separately.
The addition and subtraction signs are unaffected by the differentiation.

