Welcome to the main Calculus page. To go to a specific course, please click on the one of the links under the calculus tab above. Here’s a description of course topics.
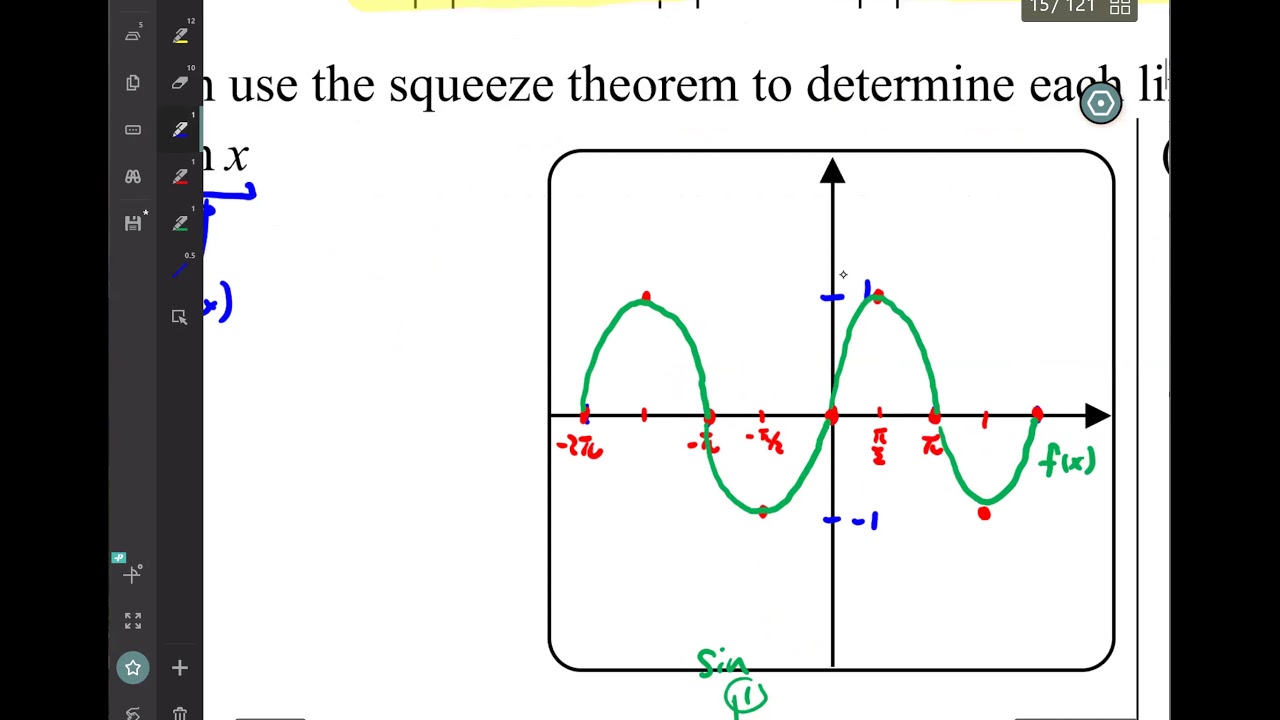
Assignments AB 2020-2021. 1.01 Numerical Limits. 1.02 Graphical Limits. 1.03 Algebraic Limits. 1.04 Squeeze Theorem. Lesson: The Squeeze Theorem Mathematics. Higher Education In this lesson, we will learn how to use the squeeze (sandwich) theorem to evaluate some limits when the value of a function is bounded by the values of two other functions.

Calculus 1

Limits – We start off by asking the fundamental question about functions. “How do we find values for points that are undefined?” After learning algebraic and analytic methods to figure this question out, as well as the Squeeze Theorem, we use limits and tangent lines to find the instantaneous rate of change, also known as the derivative.
Derivatives – Taking limits is a very tedious task, so we introduce some rules for taking derivatives. We touch on the power rule, product rule, quotient rule, and chain rule, as well as learning derivatives for trigonometry, logs, and exponents. After learning these basic techniques, we look at implicit differentiation and logarithmic differentiation, covering the derivatives that are just too hard to do with the basic techniques.

Applications – Once we cover the basics, we look at related rates. How fast is a balloon shrinking? How fast do two cars approach each other? Then we move on to maximizing and minimizing profits. We are able to find the cheapest way to design a can of cola to hold 355ml of your favorite drink. We also look at some methods of estimating roots, and an even easier way to solve limits with L’Hopital’s Rule.
Coordinate Systems and Antidifferentiation – Once we finish our applications, we touch on some of the things we will use in Calculus 2 for integration. We do parametric equations, polar coordinates, and antiderivatives.
Squeeze Theorem Ap Calculus Ab
Calculus 2
Areas – We begin by discussing areas, defining the definite integral, and proving the Fundamental Theorem of Calculus that links derivatives and integrals together.
Integration Techniques – Unfortunately, integrals aren’t very easy to compute, so we look at a variety of integration techniques to help us solve integrals.

Squeeze Theorem Ap Calculus
Applications – (In Progress)
